引用本文: 陳浩然, 劉夏陽, 王敏, 楊林, 王嘉陽, 孫海霞, 段永恒, 吳旭生, 尚麗, 錢慶, 和曉峰, 李姣. 機器學習模型在非比例風險生存資料中的應用及案例實踐. 中國循證醫學雜志, 2024, 24(9): 1108-1116. doi: 10.7507/1672-2531.202401190 復制
版權信息: ?四川大學華西醫院華西期刊社《中國循證醫學雜志》版權所有,未經授權不得轉載、改編
既包含結局事件又包含生存時間的數據被稱為生存資料,又稱為時間-事件結局數據。它因同時具有定量和定性的雙重性質,可提供比單純結局事件更加豐富的數據信息。由于生存資料的這種特殊性,針對它的獨特統計分析方法被稱為生存分析。生存分析在幫助了解疾病的自然史、評估治療方法的效果、預測患者的生存期,以及指導臨床決策等方面有著重要的意義[1]。
目前的生存分析方法大致包括三個方面:① 生存過程的描述(如Kaplan-Meier曲線);② 生存過程的比較(如log-rank檢驗);③ 影響因素分析及生存預測(如Cox比例風險回歸模型,簡稱Cox回歸)[2]。log-rank檢驗和Cox回歸模型是生存資料統計分析中最常用的分析策略,但是它們應用有著重要的前提條件—等比例風險假設,而這一要求在既往應用過程中常被忽視:嚴若華等[3]發現在PubMed檢出的使用Cox回歸模型的文章中,僅有0.34%(413/121 342)提及了比例風險假定。美國心臟協會發布的心血管醫學統計報告中明確建議需要測試并報告Cox回歸模型是否違反了等比例危險假定[4]。但是在實際數據中由于大量噪聲,很難滿足這個假設條件。鑒于此,一些針對不滿足等比例風險假定生存資料的統計分析方法已經提出:① 基于log-rank檢驗或者Kaplan-Meier檢驗用于生存過程比較的衍生方法[5];② 基于傳統的Cox回歸模型用于生存預后影響因素分析的改良方法或其他創新性方法[2](表1)。然而,這些針對非比例風險生存數據提出的改良分析方法,從根本上說是為小規模、低維度的臨床研究數據服務的。盡管它們大多有著可解釋性強和易于實施等優點,但是面對大樣本數據、高維特征數據或需要探索更加復雜關聯形式的分析要求時,它們使用的范圍就相對有限[6]。
隨著精準醫學時代的到來,可以獲得的醫學數據的規模和特征的維度急劇增加,因此對分析方法提出了更高的要求[7]。作為人工智能重要分支之一的機器學習模型(包括人工神經網絡)正越來越滲透于醫藥健康研究中[8]。針對生存分析的問題,許多研究者也開發了相關機器學習模型來分析生存預后問題[9]。機器學習模型對于數據分布的限制極少,且有更大的假設空間和擬合效果,另外這些機器學習模型在處理高維特征生存大數據或者存在競爭風險生存數據方面也有著獨特的優勢[6]。許多機器學習生存模型是對Cox回歸模型的改進(如DeepSurv[10]和Modified-DeepSurv[11]),盡管它們在解決Cox回歸模型中的非線性和交互作用等挑戰方面表現出了有效性,但對于存在非比例風險的生存數據的適用性卻受到限制。
本文在解讀NPH等相關概念之后,重點概述了可以處理不滿足等比例風險假定生存資料的機器學習模型,并進行了基于機器學習模型的腦卒中患者死亡風險的案例研究,以期推動人工智能在非比例風險生存資料分析中的應用。
1 相關概念
1.1 非比例風險
Cox回歸模型使用廣泛的主要原因在于其沒有對生存時間和基礎風險函數的分布形式做任何的要求,且可以方便的求得風險比(hazard ratios,HRs)以衡量協變量的影響效應。但是Cox回歸模型需要滿足等比例風險的假設條件,在該條件下求得HRs才會在不同的生存時間保持一致。Cox回歸模型是一個半參數模型,在等比例假設下,HRs計算公式如下:
 |
等比例風險假定即HRs與時間無關,其不隨時間變化而變化。比如在針對某種藥物開展的隨機對照試驗中,試驗組和對照組的HRs在任何的隨訪時間都是相等的,即藥物的治療效應對生存率的影響不隨時間的改變而改變。而當HRs隨時間變化,則為NPH。NPH下計算的HRs僅代表隨訪期間估計的HRs的平均水平,但是這種平均估計是不準確的,尤其對于存在交叉治療效應的生存數據[12]。
1.2 非比例風險檢驗
NPH檢驗是生存資料統計分析過程中的一個重要步驟,既往研究已經揭示了不同的方法以探索是否滿足等比例風險假定,本研究在既往研究的基礎上建議依據變量類型的不同而采取不同的方法進行檢驗[2,3,12,13]:① 連續型變量:Schoenfeld殘差圖法、Martingale殘差圖法、Schoenfeld殘差和時間線性相關分析法、時依協變量假設檢驗法;② 分類型變量:Kaplan-Meier生存曲線圖、log(-log(生存概率))與log(生存時間)作圖法(log-log作圖法)、Schoenfeld殘差圖法、Schoenfeld殘差和時間線性相關分析法。此外,建議針對每個協變量至少使用兩種以上的策略以判斷其是否滿足等比例風險假設。
2 基于機器學習算法的非比例風險模型
傳統的生存分析統計方法在數據規模較小、特征維度較低及算力有限的情況下尤為適用,且由于它們能提供協變量的參數估計而可解釋性更強[14]。以針對非比例風險生存資料衍生的Cox回歸模型為例(表1),它們依舊可以提供HRs,從而很容易理解在某個時刻下個體暴露于不同危險因素狀態下的發病風險;其他創新性的方法也各有其參數估計的方法(如加速失效時間模型的time-ratio)[12]。隨著大數據時代的到來,傳統的統計分析方法由于其自身理論基礎(如假設檢驗和抽樣估計)受到了使用的限制[14]。因此許多研究者開發了基于機器學習模型的生存統計分析方法,以期利用更先進算法的優勢分析生存預后問題。本文在檢索PubMed和CNKI數據庫的基礎上,重點匯總和概述了目前已發表文獻使用較為普遍的、適用于非比例風險生存資料的機器學習模型(表2)。
2.1 一般的機器學習模型
2.1.1 隨機生存森林(random survival forests,RSF)
RSF是由Ishwaran等[15]于2008年提出的一種將隨機森林和傳統生存分析方法相結合的樹集成學習方法,是隨機森林基于右刪失生存數據的擴展。該模型采用自助法的采樣方式隨機抽取樣本形成多個二元獨立生存樹,進而將所有的樹集合形成RSF。RSF計算每課樹的累計風險函數和生存函數,并對其進行集和得到整個森林的預測值,因此可不受等比例風險假設的限制[16]。RSF算法為機器學習模型在生存資料分析中應用最廣的模型之一。李淼等[17]基于RSF模型建立了肺癌患者死亡風險的預測模型,并揭示了RSF模型不僅可用于右刪失生存數據的分析,還能發現重要的影響因素及變量之間的交互作用。
2.1.2 極端隨機生存樹(extremely randomized survival trees,ERST)
ERST模型是RSF模型的一個變種,兩者生存樹的節點分裂標準均為log-rank分數。但是與RSF相比,ERST的隨機性在計算分割的方式上更進一步。與RSF一樣,使用的是候選特征的隨機子集,但不是尋找最具區分力的特征值,而是隨機抽取每個候選特征值,并從這些隨機生成的特征值中挑選最佳的閾值來劃分生存樹。一般來說,ERST模型的方差相對于RSF進一步減少,但是偏差相對于RSF進一步增大。在某些時候,ERST模型的泛化能力比RSF更好。
2.1.3 生存支持向量機(survival support vector machines,SSVM)
在解決小到中等規模樣本、非線性及高維模式識別中表現出許多特有優勢的支持向量機模型,同樣能和生存資料結合,形成了SSVM模型[18]。SSVM模型豐富的核函數選擇為它帶來了更大的靈活性,可有效處理生存問題中的非線性、非可加性和交互作用等問題[19]。由于支持向量機模型并不要求估計參數的潛在分布形式,因此可以解決生存資料中的非比例風險假設問題。目前使用支持向量機解決生存問題主要包括三種方法:① 回歸方法:回歸方法基于支持向量回歸的思想,旨在找到一個函數,該函數使用協變量xi估計作為連續結果值的生存時間yi[20];② 排序方法:排序方法將基于支持向量機的生存分析視為具有有序目標變量的分類問題,它的目的是預測個體之間的風險等級,而不是估計生存時間[20];③ 兩者都有。Van Belle等[19]認為當需處理高維度的生存資料時,建議使用基于回歸的SSVM模型。
2.1.4 梯度提升生存分析(gradient boosting survival,GBS)
GBS模型是基于Boosting的用于右刪失生存資料的回歸樹集成模型。盡管部分開發的GBS模型仍需遵循等比例風險這一假設,但是已經呈現出適用于高維數據、可以處理協變量間復雜非線性關聯的優勢[1,21]。Hothorn等[22]將基于加速失效時間模型的逆概率刪失加權方法和梯度提升算法相結合,開發了GBS模型以解決等比例風險假設的問題。Chen等[23]基于GBS模型構造了性能良好的陰莖鱗狀細胞癌患者的死亡風險預測模型。
2.1.5 多任務邏輯回歸(multi-task logistic regression,MTLR)
不像Cox回歸模型針對風險函數建模,MTLR通過聯合多個局部的邏輯回歸模型直接對生存函數建模,這使得它可以處理右刪失和存在時間依賴效應的協變量(即不滿足等比例風險假定)的生存資料[24]:MTLR建立了一系列不同生存時間點的邏輯回歸模型,并通過包含特定于不同時間點的參數函數將這些邏輯回歸模型聯合起來,從而捕捉時間依賴的協變量的效應。Gu等[25]發現在預測癌癥患者生存風險方面,MTLR的性能優于Cox回歸模型。
2.2 深度學習模型
2.2.1 Cox-Time
Cox-time是一種基于神經網絡的相對風險模型,它規避了傳統Cox回歸模型的比例風險假設限制。Cox-time將生存時間(t)視為常規協變量,以模擬時間變量與其他協變量之間的相互作用g(t,X),這類似于時依協變量Cox模型采用的方法,其中協變量x的非比例風險效應可以通過包括時間相關協變量[如x*t和x*log(t)]來建模:
 |
Cox-time和Cox回歸模型均為基于連續時間變量的模型,因此具有無需進行生存時間離散化的優勢(表1)[26]。Yang等[27]和Adeoye等[28]利用Cox-time算法開發了結直腸癌或口腔癌患者的死亡風險預測模型。
2.2.2 DeepHit
DeepHit是一個使用深度神經網絡直接學習生存時間分布的離散時間模型。它的網絡架構是由單個共享子網和多個特定子網組成,其損失函數同時利用了生存時間和相對風險。DeepHit模型的獨特優勢是可以處理競爭風險事件:在醫學方面,競爭風險極為普遍,例如當研究的結局是心血管疾病死亡時,因其他原因導致的死亡會阻礙該結局的發生,這兩種死亡結局互為競爭風險事件。此時若依舊運用單死亡結局終點的分析方法,將會由于競爭風險事件的存在而導致對終點事件概率的估計產生偏差。目前的競爭風險模型(如原因別風險模型和Fine-Gray模型)均基于傳統統計學方法,因此基于深度學習的DeepHit模型將有更大的應用價值。
2.2.3 N-MTLR(neural multi-task logistic regression)
N-MTLR是一種基于神經網絡的模型,它在不同的時間間隔上構建不同的神經網絡來估計每個時間間隔內結局事件發生的概率[29]。N-MTLR與MTLR不同的是引入了深度學習架構,從而解決了MTLR無法對生存資料中非線性關聯建模的問題。Fotso等[29]發現,當分析存在復雜非線性關聯的生存數據時,N-MTLR的性能顯著高于Cox回歸模型和NTLR模型。Kiessling等[30]使用N-MTLR來估計選擇性腹主動脈瘤修復后的死亡風險:該研究發現N-MTLR比Kaplan-Meier方法顯示出更精確的估計,并且能夠發現Kaplan-Meier無法檢測到的患者亞組之間的生存差異。
3 案例研究
3.1 數據獲得與清洗
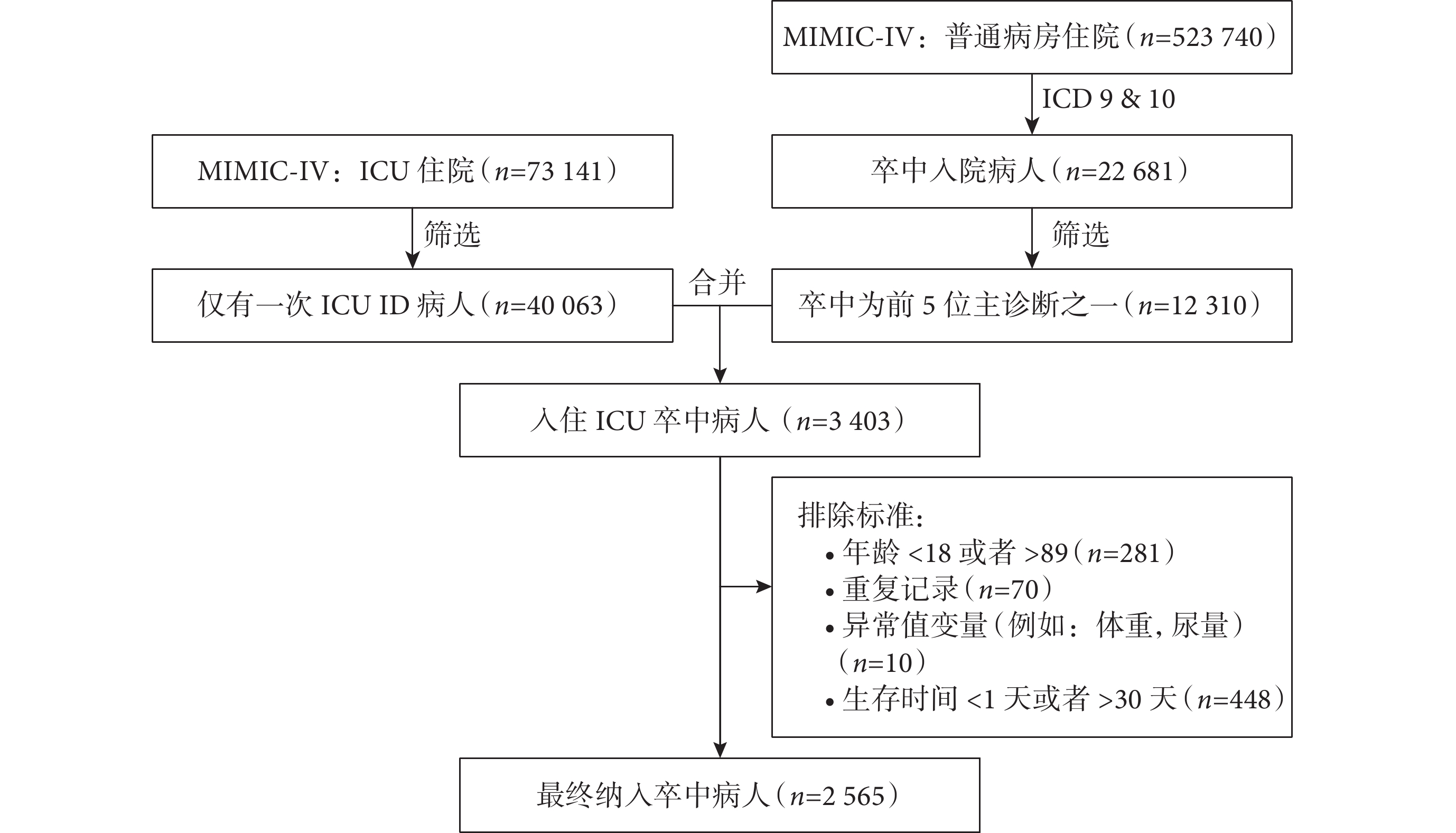
案例研究數據來自美國重癥監護醫學數據庫(Medical Information Mart for Intensive Care-Ⅳ,MIMIC-IV)。MIMIC-IV包含了2008年至2019年間美國三級學術醫療中心住院患者的臨床電子病歷的數據信息。我們使用SQL、PostgreSQL和Navicat Premium軟件提取了2 565名中風患者的數據(圖1),包括臨床特征、實驗室測量、合并癥、生命體征和疾病嚴重程度評估等68個變量(表3)。我們分別對于連續型缺失變量和分類型缺失變量進行了中位數填充和眾數填充,此外分別對分類變量和連續型變量進行了啞變量化和標準化。本文機器學習算法使用Python(version 3.8)編程語言實現。其中,兩種集成學習模型使用了sksurv軟件包(version 0.17.2),而兩種深度學習模型采用了pycox(version 0.2.3)、torch (version 1.8.0+cpu)和torchtuples(version 0.2.2)軟件包,其他的統計分析使用SAS(version 9.4)軟件實現。
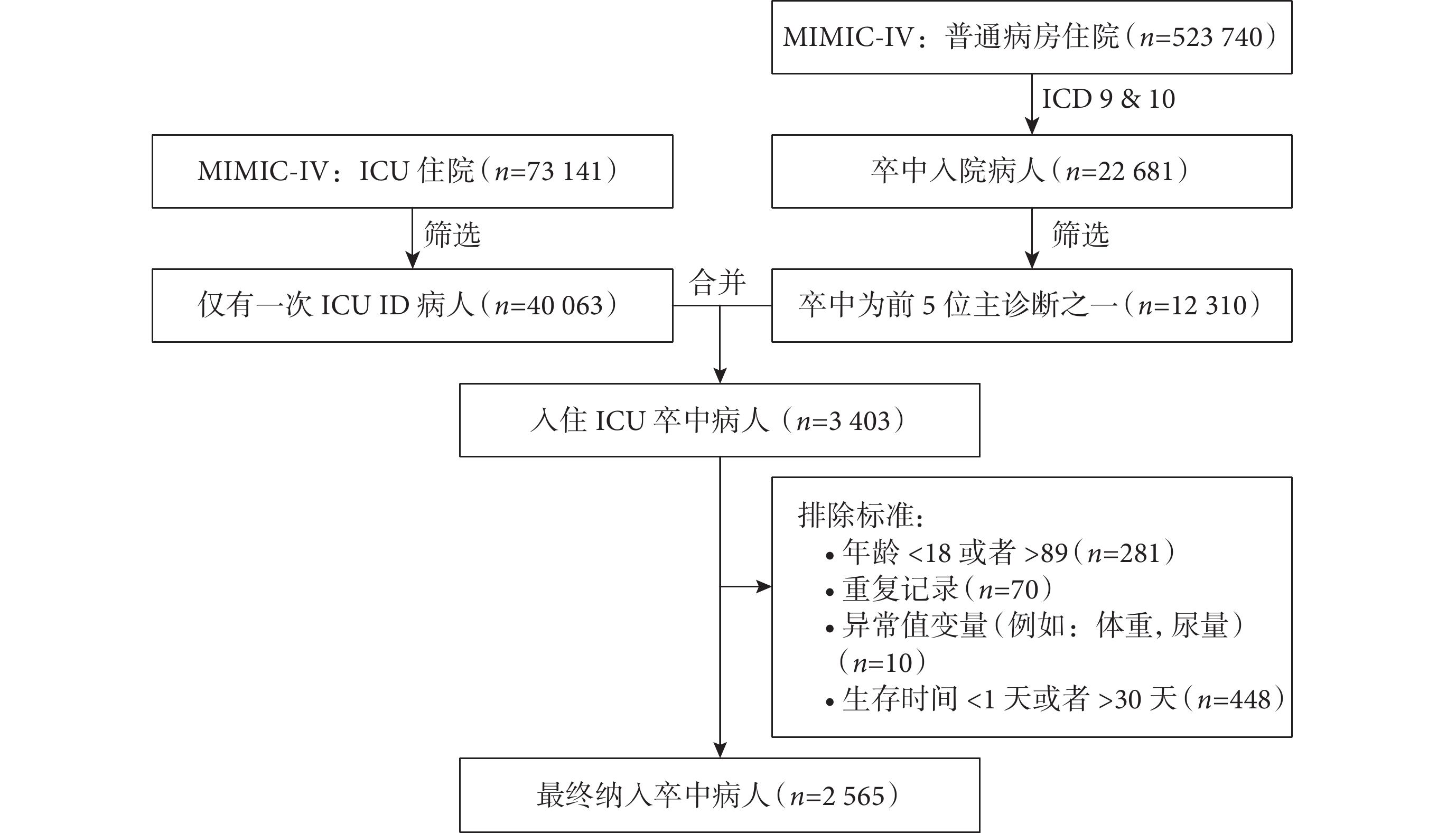 圖1
研究對象納入流程圖
圖1
研究對象納入流程圖
3.2 非比例風險檢驗
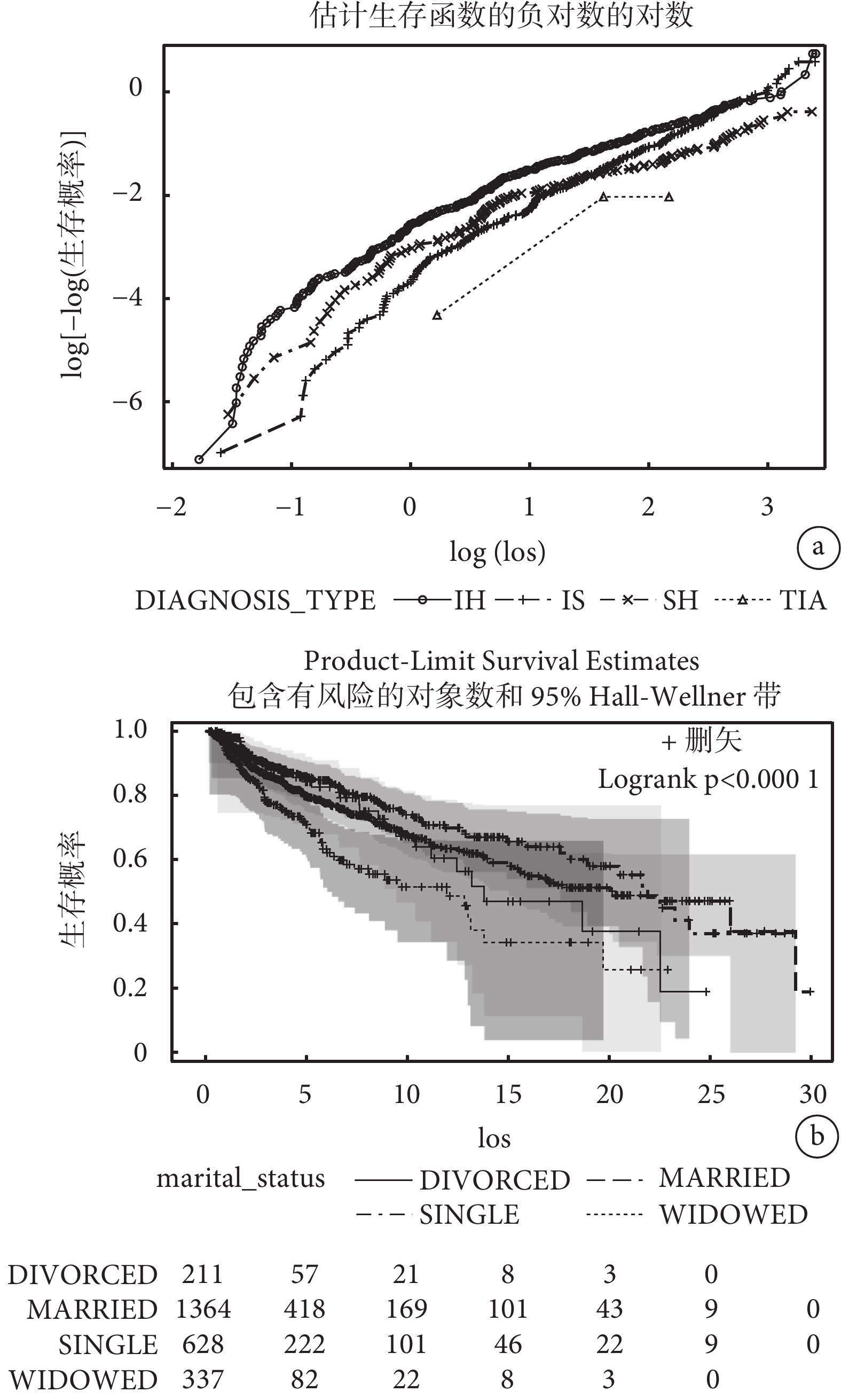
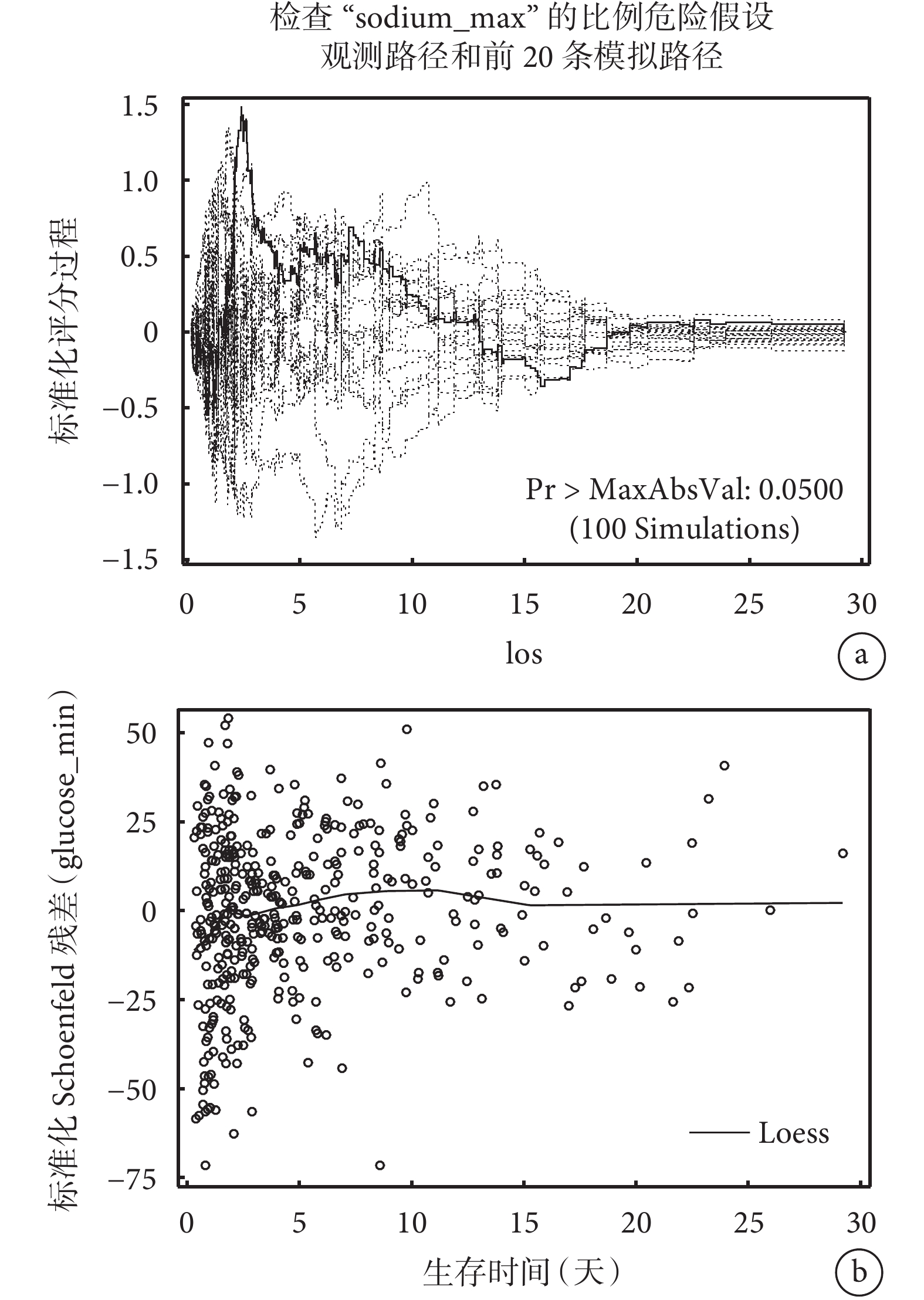
針對分類型變量和連續型變量均采用了兩種方法檢驗等比例風險假設(結果見表4、圖2和圖3):表4中Schoenfeld殘差和生存時間線性相關法檢驗顯示兩個分類型變量(DIAGNOSIS_TYPE、marital_status)和兩個連續型變量(max_sodium、min_glucose)均不滿足等比例風假定(P<0.001);圖2 log(?log(生存概率))與log(生存時間)圖形顯示不同的卒中診斷類型曲線交叉,不同婚姻狀態的生存曲線同樣顯示交叉,這表明它們的等比例風險假設不成立;圖3 Martingale殘差圖中sodium_max的實際路徑在模擬路徑之外,glucose_min的schoenfeld殘差圖在生存時間少于15天內的線性斜率不等于0,這表明不滿足等比例風險假設。以上分析結果表明案例卒中生存資料不滿足等比例風險假設,因此我們采用適用于非比例風險假設的機器學習和深度學習生存分析算法進行腦卒中死亡風險預測。
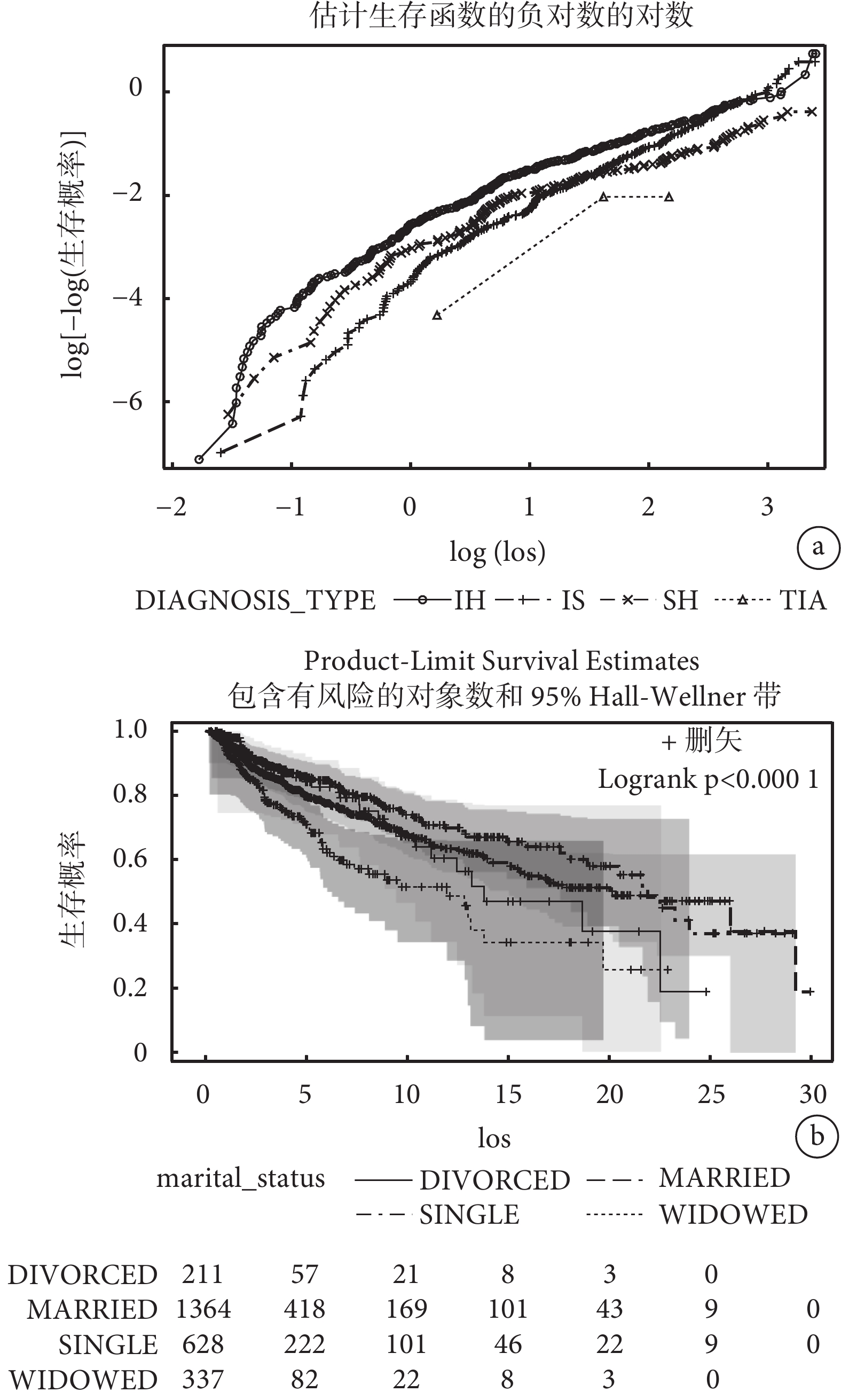 圖2
分類型變量比例風險假定檢驗
圖2
分類型變量比例風險假定檢驗
a:“DIAGNOSIS_TYPE”變量log-log作圖法;b:“marital_status”變量生存曲線作圖法。
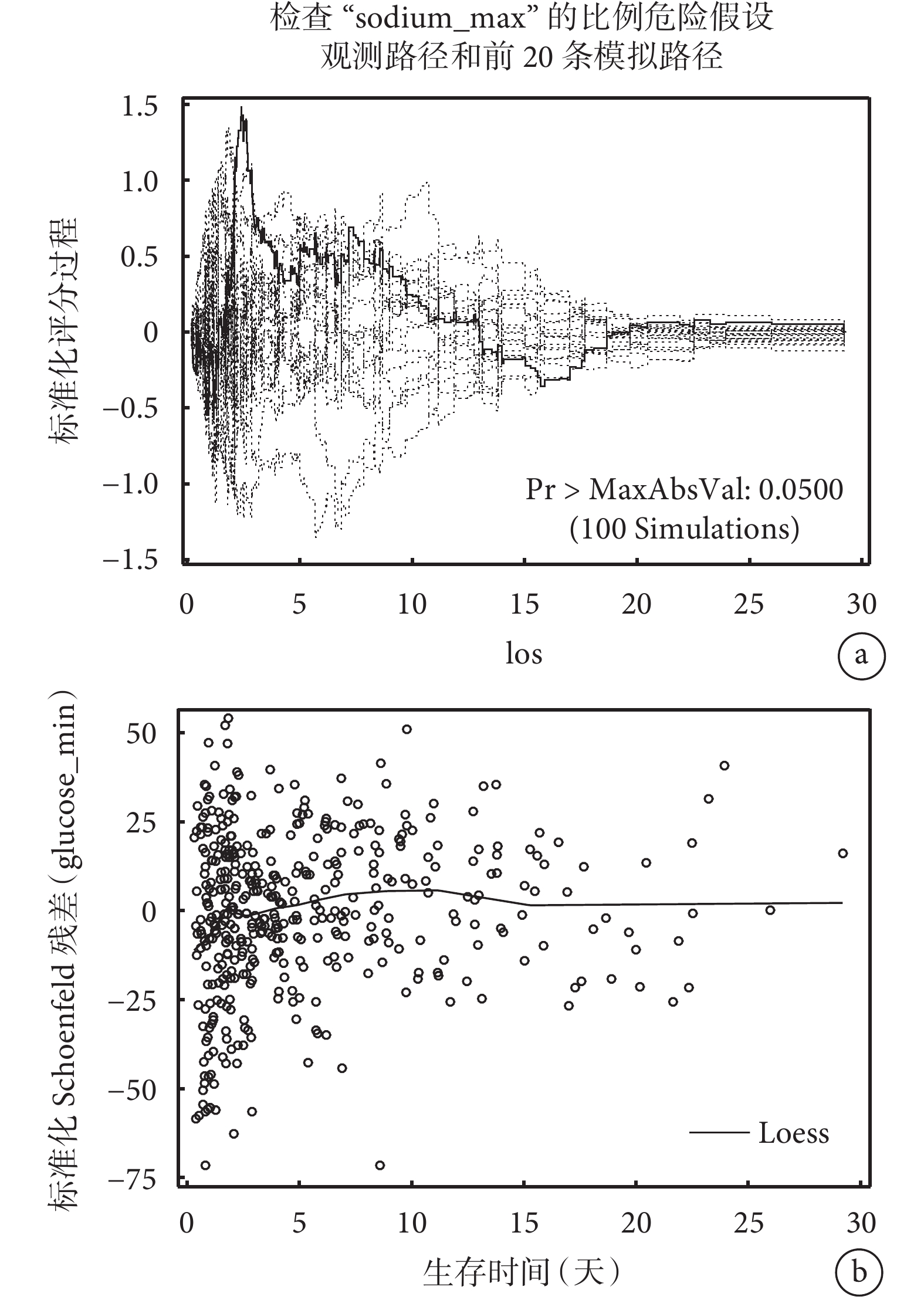 圖3
連續型變量比例風險假定檢驗
圖3
連續型變量比例風險假定檢驗
a:“sodium_max”變量Martingale殘差圖法;b:“glucose_min”變量Schoenfeld殘差圖法。
3.3 模型構建與評價
對于處理后的數據分別使用兩種集成學習模型(隨機生存森林和極端生存樹)和兩種深度學習模型(Cox-time和DeepHit)構建腦卒中死亡風險預測模型。模型的訓練采用留出法(訓練集∶測試集=7∶3),即在訓練集上訓練模型,在測試集上評價模型的性能。本研究使用Harrell’s 一致性指數(concordance index,C-index)對比不同模型的區分度[31];使用積分布里爾評分(integrated brier score,IBS)對比不同模型的校準度[32]。本研究沒有對各模型的超參數進行調整,即使用它們的默認超參數。除此之外,針對表現最好的隨機生存森林模型采用排列重要性(permutation importance)的方法識別影響腦卒中患者死亡風險的重要特征[33]。
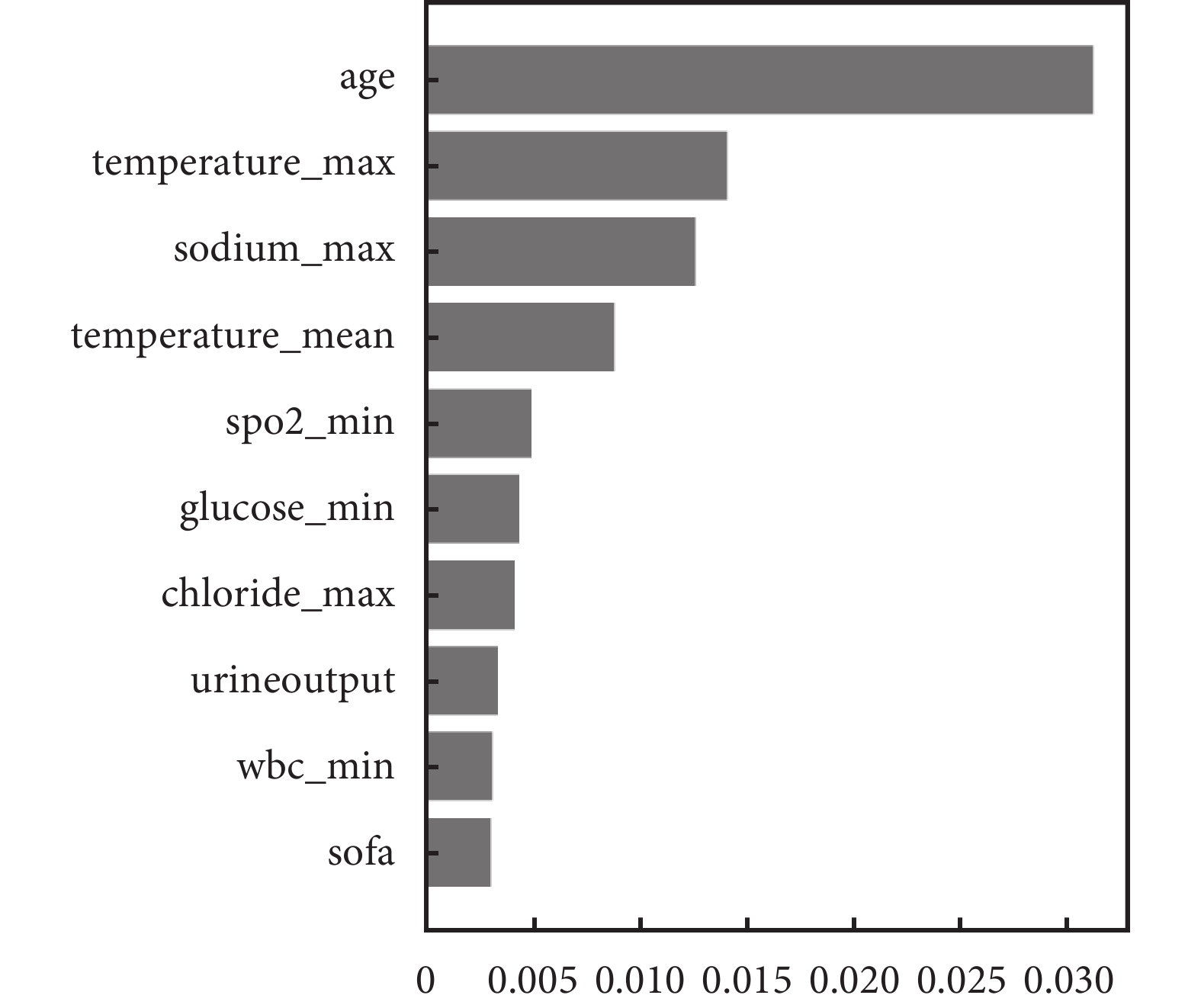
表5顯示集成機器學習模型的區分度性能和校準度性能均更好:其中隨機生存森林的區分度性能最高(C-index=0.773),且其校準度也更好(IBS=0.151)。基于神經網絡的算法Cox-time和DeepHit表現相對較差,這可能是由于本案例研究數據規模相對較小且沒有調節深度學習生存模型超參數。基于排列重要性算法得出影響腦卒中ICU住院患者死亡風險重要的特征包括年齡和日最大體溫等(圖4),這也與既往研究的發現一致[34, 35]。
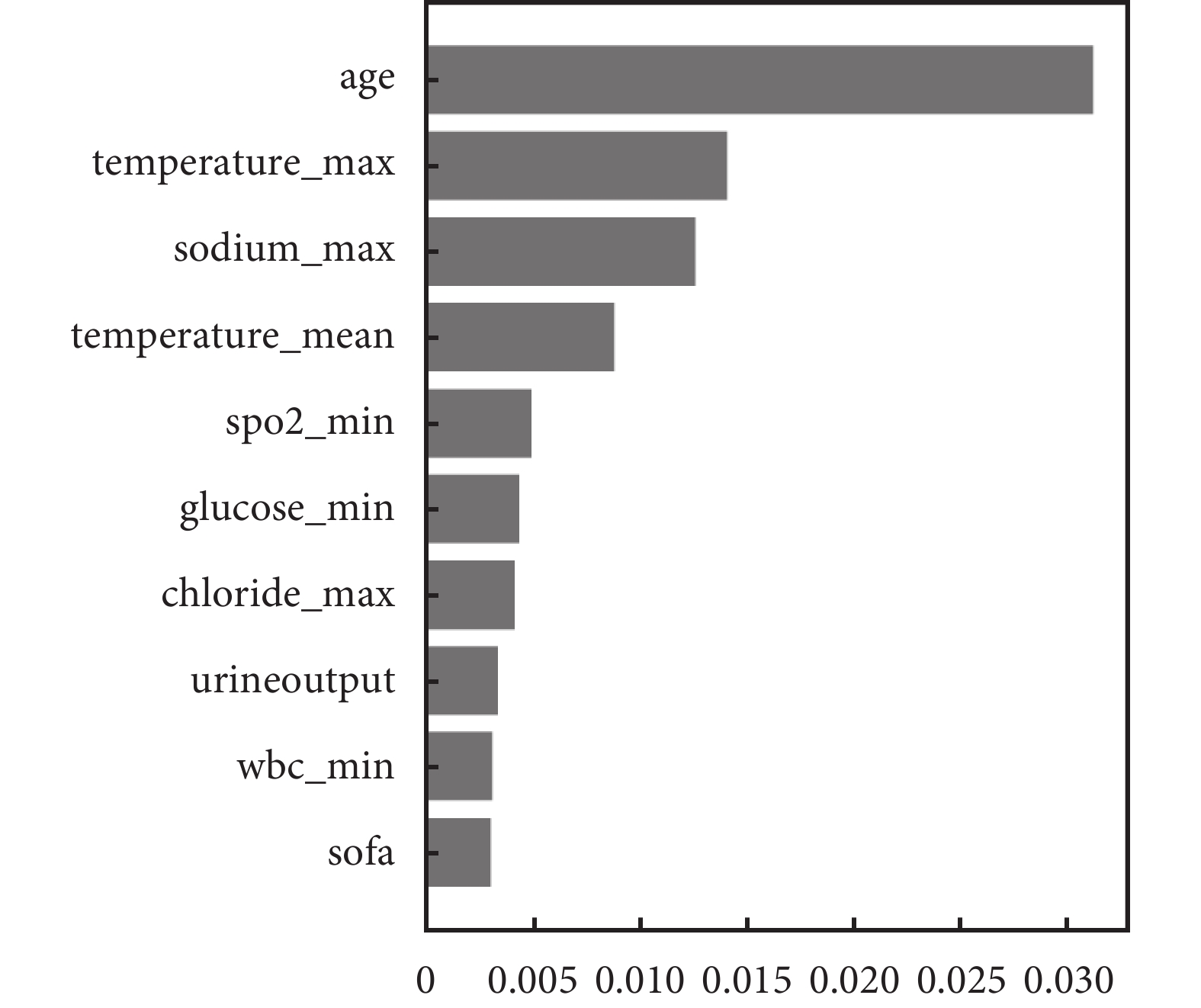 圖4
基于排列重要性算法獲得的影響腦卒中患者死亡風險的前10個重要變量
圖4
基于排列重要性算法獲得的影響腦卒中患者死亡風險的前10個重要變量
4 討論
Cox比例風險模型是生存分析中最常用的模型之一,它基于等比例風險假定,可以有效地分析生存數據并得出相關結論。如果生存數據不符合等比例風險假定,那么使用Cox比例風險模型進行分析就是不合適的,研究人員需要考慮其他的生存分析方法。但是傳統的非比例風險生存分析方法存在無法對非線性關聯建模和不適用于高維數據的固有缺陷[9]。鑒于人工智能在處理醫學大數據方面的巨大作用,許多研究者將機器學習應用到生存分析領域并開發出了性能優良算法。因此本文系統概述了適用于非比例風險生存資料的機器學習生存模型并比較了各種模型的優缺點。并以腦卒中患者死亡風險研究作為研究實例比較了多種機器學習模型的預測性能,從而強調了這些機器算法在生存分析研究中應有更多的應用機會。
生存資料的NPH檢驗問題近些年得到越來越多的關注,主要原因在于統計學家發現腫瘤免疫靶向藥物的臨床試驗的生存資料大多并不滿足等比例風險假定(呈現延遲治療效應)[36],因此早在2018年就于杜克大學舉辦的“存在非比例危害的腫瘤學臨床試驗”會議中提出要開發新的統計方法[37]。但是長久以來開發的傳統的非比例風險生存分析方法可能只適合于臨床試驗的統計分析,主要在于臨床試驗的數據規模和變量數目都小得多。而在如今的精準醫學時代,數據的規模、維度和復雜程度都呈現急劇增加,尤其是一些組學數據還呈現出特征維度遠遠高于數據量大小的特點,這給既往的非比例生存分析方法帶來了巨大的挑戰[6]。
Huang等[9]首次開展了將機器學習的方法應用于生存預后分析方面文獻的綜述,這篇研究對各種機器學習生存分析模型給出了詳細的介紹,但是依舊沒有關注到這些模型是否適用于非比例風險生存資料。而本研究彌補了這一疏漏之處—重點匯總了適用于非比例風險生存資料的機器學習模型。除此之外,本研究還基于真實世界數據對等比例風險假定的檢驗方法和機器學習生存模型做了實例探索,以期為研究人員開展類似研究提供更多的參考價值。本文案例研究的目的并不是澄清最優的機器學習生存分析模型,因此并未對各個模型的超參數進行調整。相反,為生存分析選擇最合適的機器學習模型應該基于自身的研究問題、數據集規模、特征維度或數據集的平衡程度等方面。
盡管基于機器學習的模型因其具備更強的處理高維數據能力和數據靈活性等優勢,在預測復雜生存數據方面可能表現更佳,但相較于傳統的非比例風險生存分析方法,我們認為它們在以下幾個方面存在明顯的局限性:1)模型的可解釋性:由于傳統的非比例風險生存分析方法主要在于因果關系的解釋,而基于機器學習的非比例風險生存分析方法在于結局預測,因此它們的結果可解釋性遠不如HRs易于理解和接受[38]。現有的機器學習可解釋性方法也較局限[39],其解釋結果依然不夠清晰(如圖4),將來的機器學習生存算法應在提高臨床決策可解釋性方面得到進一步發展。2)更大的樣本量需求[40, 41]:在將基于機器學習的分析方法應用于復雜的生存資料時尤為顯著,主要由以下幾個內外部因素引起:① 機器學習模型的復雜性增加(例如,深度學習模型具有大量參數和非線性結構),因此為了確保模型能夠有效地泛化和保持穩定性,通常需要更大的樣本量;② 復雜的生存資料涉及更高維度的特征空間,因此需要更多的樣本以充分覆蓋特征空間,以避免過度擬合或欠擬合;③ 機器學習模型通常需要更多的數據進行有效的訓練和調優,這包括捕獲數據中的模式和規律,以及進行參數調整以提高性能;④ 機器學習模型對數據中的噪聲和復雜性更為敏感,更大的樣本量能夠提供更多信息,幫助模型準確區分真實模式和噪聲,從而提高魯棒性和泛化能力。3)過擬合風險高[42]:由于機器學習模型具有足夠的靈活性和參數數量,可以幾乎完美地擬合訓練數據,甚至是其中的噪聲,這種過度擬合會導致模型在訓練數據上表現良好,但在新數據上表現不佳。相比之下,傳統的生存分析模型在一定程度上更加穩定,過擬合的風險較低。關于機器學習的模型更強調采取如交叉驗證、正則化等方式以減少過擬合的風險[43]。除了上述局限性之外,基于機器學習的生存分析模型也存在參數調優困難[44]、計算資源需求高[45]和穩定性差[46]等缺陷。
既包含結局事件又包含生存時間的數據被稱為生存資料,又稱為時間-事件結局數據。它因同時具有定量和定性的雙重性質,可提供比單純結局事件更加豐富的數據信息。由于生存資料的這種特殊性,針對它的獨特統計分析方法被稱為生存分析。生存分析在幫助了解疾病的自然史、評估治療方法的效果、預測患者的生存期,以及指導臨床決策等方面有著重要的意義[1]。
目前的生存分析方法大致包括三個方面:① 生存過程的描述(如Kaplan-Meier曲線);② 生存過程的比較(如log-rank檢驗);③ 影響因素分析及生存預測(如Cox比例風險回歸模型,簡稱Cox回歸)[2]。log-rank檢驗和Cox回歸模型是生存資料統計分析中最常用的分析策略,但是它們應用有著重要的前提條件—等比例風險假設,而這一要求在既往應用過程中常被忽視:嚴若華等[3]發現在PubMed檢出的使用Cox回歸模型的文章中,僅有0.34%(413/121 342)提及了比例風險假定。美國心臟協會發布的心血管醫學統計報告中明確建議需要測試并報告Cox回歸模型是否違反了等比例危險假定[4]。但是在實際數據中由于大量噪聲,很難滿足這個假設條件。鑒于此,一些針對不滿足等比例風險假定生存資料的統計分析方法已經提出:① 基于log-rank檢驗或者Kaplan-Meier檢驗用于生存過程比較的衍生方法[5];② 基于傳統的Cox回歸模型用于生存預后影響因素分析的改良方法或其他創新性方法[2](表1)。然而,這些針對非比例風險生存數據提出的改良分析方法,從根本上說是為小規模、低維度的臨床研究數據服務的。盡管它們大多有著可解釋性強和易于實施等優點,但是面對大樣本數據、高維特征數據或需要探索更加復雜關聯形式的分析要求時,它們使用的范圍就相對有限[6]。
隨著精準醫學時代的到來,可以獲得的醫學數據的規模和特征的維度急劇增加,因此對分析方法提出了更高的要求[7]。作為人工智能重要分支之一的機器學習模型(包括人工神經網絡)正越來越滲透于醫藥健康研究中[8]。針對生存分析的問題,許多研究者也開發了相關機器學習模型來分析生存預后問題[9]。機器學習模型對于數據分布的限制極少,且有更大的假設空間和擬合效果,另外這些機器學習模型在處理高維特征生存大數據或者存在競爭風險生存數據方面也有著獨特的優勢[6]。許多機器學習生存模型是對Cox回歸模型的改進(如DeepSurv[10]和Modified-DeepSurv[11]),盡管它們在解決Cox回歸模型中的非線性和交互作用等挑戰方面表現出了有效性,但對于存在非比例風險的生存數據的適用性卻受到限制。
本文在解讀NPH等相關概念之后,重點概述了可以處理不滿足等比例風險假定生存資料的機器學習模型,并進行了基于機器學習模型的腦卒中患者死亡風險的案例研究,以期推動人工智能在非比例風險生存資料分析中的應用。
1 相關概念
1.1 非比例風險
Cox回歸模型使用廣泛的主要原因在于其沒有對生存時間和基礎風險函數的分布形式做任何的要求,且可以方便的求得風險比(hazard ratios,HRs)以衡量協變量的影響效應。但是Cox回歸模型需要滿足等比例風險的假設條件,在該條件下求得HRs才會在不同的生存時間保持一致。Cox回歸模型是一個半參數模型,在等比例假設下,HRs計算公式如下:
 |
等比例風險假定即HRs與時間無關,其不隨時間變化而變化。比如在針對某種藥物開展的隨機對照試驗中,試驗組和對照組的HRs在任何的隨訪時間都是相等的,即藥物的治療效應對生存率的影響不隨時間的改變而改變。而當HRs隨時間變化,則為NPH。NPH下計算的HRs僅代表隨訪期間估計的HRs的平均水平,但是這種平均估計是不準確的,尤其對于存在交叉治療效應的生存數據[12]。
1.2 非比例風險檢驗
NPH檢驗是生存資料統計分析過程中的一個重要步驟,既往研究已經揭示了不同的方法以探索是否滿足等比例風險假定,本研究在既往研究的基礎上建議依據變量類型的不同而采取不同的方法進行檢驗[2,3,12,13]:① 連續型變量:Schoenfeld殘差圖法、Martingale殘差圖法、Schoenfeld殘差和時間線性相關分析法、時依協變量假設檢驗法;② 分類型變量:Kaplan-Meier生存曲線圖、log(-log(生存概率))與log(生存時間)作圖法(log-log作圖法)、Schoenfeld殘差圖法、Schoenfeld殘差和時間線性相關分析法。此外,建議針對每個協變量至少使用兩種以上的策略以判斷其是否滿足等比例風險假設。
2 基于機器學習算法的非比例風險模型
傳統的生存分析統計方法在數據規模較小、特征維度較低及算力有限的情況下尤為適用,且由于它們能提供協變量的參數估計而可解釋性更強[14]。以針對非比例風險生存資料衍生的Cox回歸模型為例(表1),它們依舊可以提供HRs,從而很容易理解在某個時刻下個體暴露于不同危險因素狀態下的發病風險;其他創新性的方法也各有其參數估計的方法(如加速失效時間模型的time-ratio)[12]。隨著大數據時代的到來,傳統的統計分析方法由于其自身理論基礎(如假設檢驗和抽樣估計)受到了使用的限制[14]。因此許多研究者開發了基于機器學習模型的生存統計分析方法,以期利用更先進算法的優勢分析生存預后問題。本文在檢索PubMed和CNKI數據庫的基礎上,重點匯總和概述了目前已發表文獻使用較為普遍的、適用于非比例風險生存資料的機器學習模型(表2)。
2.1 一般的機器學習模型
2.1.1 隨機生存森林(random survival forests,RSF)
RSF是由Ishwaran等[15]于2008年提出的一種將隨機森林和傳統生存分析方法相結合的樹集成學習方法,是隨機森林基于右刪失生存數據的擴展。該模型采用自助法的采樣方式隨機抽取樣本形成多個二元獨立生存樹,進而將所有的樹集合形成RSF。RSF計算每課樹的累計風險函數和生存函數,并對其進行集和得到整個森林的預測值,因此可不受等比例風險假設的限制[16]。RSF算法為機器學習模型在生存資料分析中應用最廣的模型之一。李淼等[17]基于RSF模型建立了肺癌患者死亡風險的預測模型,并揭示了RSF模型不僅可用于右刪失生存數據的分析,還能發現重要的影響因素及變量之間的交互作用。
2.1.2 極端隨機生存樹(extremely randomized survival trees,ERST)
ERST模型是RSF模型的一個變種,兩者生存樹的節點分裂標準均為log-rank分數。但是與RSF相比,ERST的隨機性在計算分割的方式上更進一步。與RSF一樣,使用的是候選特征的隨機子集,但不是尋找最具區分力的特征值,而是隨機抽取每個候選特征值,并從這些隨機生成的特征值中挑選最佳的閾值來劃分生存樹。一般來說,ERST模型的方差相對于RSF進一步減少,但是偏差相對于RSF進一步增大。在某些時候,ERST模型的泛化能力比RSF更好。
2.1.3 生存支持向量機(survival support vector machines,SSVM)
在解決小到中等規模樣本、非線性及高維模式識別中表現出許多特有優勢的支持向量機模型,同樣能和生存資料結合,形成了SSVM模型[18]。SSVM模型豐富的核函數選擇為它帶來了更大的靈活性,可有效處理生存問題中的非線性、非可加性和交互作用等問題[19]。由于支持向量機模型并不要求估計參數的潛在分布形式,因此可以解決生存資料中的非比例風險假設問題。目前使用支持向量機解決生存問題主要包括三種方法:① 回歸方法:回歸方法基于支持向量回歸的思想,旨在找到一個函數,該函數使用協變量xi估計作為連續結果值的生存時間yi[20];② 排序方法:排序方法將基于支持向量機的生存分析視為具有有序目標變量的分類問題,它的目的是預測個體之間的風險等級,而不是估計生存時間[20];③ 兩者都有。Van Belle等[19]認為當需處理高維度的生存資料時,建議使用基于回歸的SSVM模型。
2.1.4 梯度提升生存分析(gradient boosting survival,GBS)
GBS模型是基于Boosting的用于右刪失生存資料的回歸樹集成模型。盡管部分開發的GBS模型仍需遵循等比例風險這一假設,但是已經呈現出適用于高維數據、可以處理協變量間復雜非線性關聯的優勢[1,21]。Hothorn等[22]將基于加速失效時間模型的逆概率刪失加權方法和梯度提升算法相結合,開發了GBS模型以解決等比例風險假設的問題。Chen等[23]基于GBS模型構造了性能良好的陰莖鱗狀細胞癌患者的死亡風險預測模型。
2.1.5 多任務邏輯回歸(multi-task logistic regression,MTLR)
不像Cox回歸模型針對風險函數建模,MTLR通過聯合多個局部的邏輯回歸模型直接對生存函數建模,這使得它可以處理右刪失和存在時間依賴效應的協變量(即不滿足等比例風險假定)的生存資料[24]:MTLR建立了一系列不同生存時間點的邏輯回歸模型,并通過包含特定于不同時間點的參數函數將這些邏輯回歸模型聯合起來,從而捕捉時間依賴的協變量的效應。Gu等[25]發現在預測癌癥患者生存風險方面,MTLR的性能優于Cox回歸模型。
2.2 深度學習模型
2.2.1 Cox-Time
Cox-time是一種基于神經網絡的相對風險模型,它規避了傳統Cox回歸模型的比例風險假設限制。Cox-time將生存時間(t)視為常規協變量,以模擬時間變量與其他協變量之間的相互作用g(t,X),這類似于時依協變量Cox模型采用的方法,其中協變量x的非比例風險效應可以通過包括時間相關協變量[如x*t和x*log(t)]來建模:
 |
Cox-time和Cox回歸模型均為基于連續時間變量的模型,因此具有無需進行生存時間離散化的優勢(表1)[26]。Yang等[27]和Adeoye等[28]利用Cox-time算法開發了結直腸癌或口腔癌患者的死亡風險預測模型。
2.2.2 DeepHit
DeepHit是一個使用深度神經網絡直接學習生存時間分布的離散時間模型。它的網絡架構是由單個共享子網和多個特定子網組成,其損失函數同時利用了生存時間和相對風險。DeepHit模型的獨特優勢是可以處理競爭風險事件:在醫學方面,競爭風險極為普遍,例如當研究的結局是心血管疾病死亡時,因其他原因導致的死亡會阻礙該結局的發生,這兩種死亡結局互為競爭風險事件。此時若依舊運用單死亡結局終點的分析方法,將會由于競爭風險事件的存在而導致對終點事件概率的估計產生偏差。目前的競爭風險模型(如原因別風險模型和Fine-Gray模型)均基于傳統統計學方法,因此基于深度學習的DeepHit模型將有更大的應用價值。
2.2.3 N-MTLR(neural multi-task logistic regression)
N-MTLR是一種基于神經網絡的模型,它在不同的時間間隔上構建不同的神經網絡來估計每個時間間隔內結局事件發生的概率[29]。N-MTLR與MTLR不同的是引入了深度學習架構,從而解決了MTLR無法對生存資料中非線性關聯建模的問題。Fotso等[29]發現,當分析存在復雜非線性關聯的生存數據時,N-MTLR的性能顯著高于Cox回歸模型和NTLR模型。Kiessling等[30]使用N-MTLR來估計選擇性腹主動脈瘤修復后的死亡風險:該研究發現N-MTLR比Kaplan-Meier方法顯示出更精確的估計,并且能夠發現Kaplan-Meier無法檢測到的患者亞組之間的生存差異。
3 案例研究
3.1 數據獲得與清洗
案例研究數據來自美國重癥監護醫學數據庫(Medical Information Mart for Intensive Care-Ⅳ,MIMIC-IV)。MIMIC-IV包含了2008年至2019年間美國三級學術醫療中心住院患者的臨床電子病歷的數據信息。我們使用SQL、PostgreSQL和Navicat Premium軟件提取了2 565名中風患者的數據(圖1),包括臨床特征、實驗室測量、合并癥、生命體征和疾病嚴重程度評估等68個變量(表3)。我們分別對于連續型缺失變量和分類型缺失變量進行了中位數填充和眾數填充,此外分別對分類變量和連續型變量進行了啞變量化和標準化。本文機器學習算法使用Python(version 3.8)編程語言實現。其中,兩種集成學習模型使用了sksurv軟件包(version 0.17.2),而兩種深度學習模型采用了pycox(version 0.2.3)、torch (version 1.8.0+cpu)和torchtuples(version 0.2.2)軟件包,其他的統計分析使用SAS(version 9.4)軟件實現。
 圖1
研究對象納入流程圖
圖1
研究對象納入流程圖
3.2 非比例風險檢驗
針對分類型變量和連續型變量均采用了兩種方法檢驗等比例風險假設(結果見表4、圖2和圖3):表4中Schoenfeld殘差和生存時間線性相關法檢驗顯示兩個分類型變量(DIAGNOSIS_TYPE、marital_status)和兩個連續型變量(max_sodium、min_glucose)均不滿足等比例風假定(P<0.001);圖2 log(?log(生存概率))與log(生存時間)圖形顯示不同的卒中診斷類型曲線交叉,不同婚姻狀態的生存曲線同樣顯示交叉,這表明它們的等比例風險假設不成立;圖3 Martingale殘差圖中sodium_max的實際路徑在模擬路徑之外,glucose_min的schoenfeld殘差圖在生存時間少于15天內的線性斜率不等于0,這表明不滿足等比例風險假設。以上分析結果表明案例卒中生存資料不滿足等比例風險假設,因此我們采用適用于非比例風險假設的機器學習和深度學習生存分析算法進行腦卒中死亡風險預測。
 圖2
分類型變量比例風險假定檢驗
圖2
分類型變量比例風險假定檢驗
a:“DIAGNOSIS_TYPE”變量log-log作圖法;b:“marital_status”變量生存曲線作圖法。
 圖3
連續型變量比例風險假定檢驗
圖3
連續型變量比例風險假定檢驗
a:“sodium_max”變量Martingale殘差圖法;b:“glucose_min”變量Schoenfeld殘差圖法。
3.3 模型構建與評價
對于處理后的數據分別使用兩種集成學習模型(隨機生存森林和極端生存樹)和兩種深度學習模型(Cox-time和DeepHit)構建腦卒中死亡風險預測模型。模型的訓練采用留出法(訓練集∶測試集=7∶3),即在訓練集上訓練模型,在測試集上評價模型的性能。本研究使用Harrell’s 一致性指數(concordance index,C-index)對比不同模型的區分度[31];使用積分布里爾評分(integrated brier score,IBS)對比不同模型的校準度[32]。本研究沒有對各模型的超參數進行調整,即使用它們的默認超參數。除此之外,針對表現最好的隨機生存森林模型采用排列重要性(permutation importance)的方法識別影響腦卒中患者死亡風險的重要特征[33]。
表5顯示集成機器學習模型的區分度性能和校準度性能均更好:其中隨機生存森林的區分度性能最高(C-index=0.773),且其校準度也更好(IBS=0.151)。基于神經網絡的算法Cox-time和DeepHit表現相對較差,這可能是由于本案例研究數據規模相對較小且沒有調節深度學習生存模型超參數。基于排列重要性算法得出影響腦卒中ICU住院患者死亡風險重要的特征包括年齡和日最大體溫等(圖4),這也與既往研究的發現一致[34, 35]。
 圖4
基于排列重要性算法獲得的影響腦卒中患者死亡風險的前10個重要變量
圖4
基于排列重要性算法獲得的影響腦卒中患者死亡風險的前10個重要變量
4 討論
Cox比例風險模型是生存分析中最常用的模型之一,它基于等比例風險假定,可以有效地分析生存數據并得出相關結論。如果生存數據不符合等比例風險假定,那么使用Cox比例風險模型進行分析就是不合適的,研究人員需要考慮其他的生存分析方法。但是傳統的非比例風險生存分析方法存在無法對非線性關聯建模和不適用于高維數據的固有缺陷[9]。鑒于人工智能在處理醫學大數據方面的巨大作用,許多研究者將機器學習應用到生存分析領域并開發出了性能優良算法。因此本文系統概述了適用于非比例風險生存資料的機器學習生存模型并比較了各種模型的優缺點。并以腦卒中患者死亡風險研究作為研究實例比較了多種機器學習模型的預測性能,從而強調了這些機器算法在生存分析研究中應有更多的應用機會。
生存資料的NPH檢驗問題近些年得到越來越多的關注,主要原因在于統計學家發現腫瘤免疫靶向藥物的臨床試驗的生存資料大多并不滿足等比例風險假定(呈現延遲治療效應)[36],因此早在2018年就于杜克大學舉辦的“存在非比例危害的腫瘤學臨床試驗”會議中提出要開發新的統計方法[37]。但是長久以來開發的傳統的非比例風險生存分析方法可能只適合于臨床試驗的統計分析,主要在于臨床試驗的數據規模和變量數目都小得多。而在如今的精準醫學時代,數據的規模、維度和復雜程度都呈現急劇增加,尤其是一些組學數據還呈現出特征維度遠遠高于數據量大小的特點,這給既往的非比例生存分析方法帶來了巨大的挑戰[6]。
Huang等[9]首次開展了將機器學習的方法應用于生存預后分析方面文獻的綜述,這篇研究對各種機器學習生存分析模型給出了詳細的介紹,但是依舊沒有關注到這些模型是否適用于非比例風險生存資料。而本研究彌補了這一疏漏之處—重點匯總了適用于非比例風險生存資料的機器學習模型。除此之外,本研究還基于真實世界數據對等比例風險假定的檢驗方法和機器學習生存模型做了實例探索,以期為研究人員開展類似研究提供更多的參考價值。本文案例研究的目的并不是澄清最優的機器學習生存分析模型,因此并未對各個模型的超參數進行調整。相反,為生存分析選擇最合適的機器學習模型應該基于自身的研究問題、數據集規模、特征維度或數據集的平衡程度等方面。
盡管基于機器學習的模型因其具備更強的處理高維數據能力和數據靈活性等優勢,在預測復雜生存數據方面可能表現更佳,但相較于傳統的非比例風險生存分析方法,我們認為它們在以下幾個方面存在明顯的局限性:1)模型的可解釋性:由于傳統的非比例風險生存分析方法主要在于因果關系的解釋,而基于機器學習的非比例風險生存分析方法在于結局預測,因此它們的結果可解釋性遠不如HRs易于理解和接受[38]。現有的機器學習可解釋性方法也較局限[39],其解釋結果依然不夠清晰(如圖4),將來的機器學習生存算法應在提高臨床決策可解釋性方面得到進一步發展。2)更大的樣本量需求[40, 41]:在將基于機器學習的分析方法應用于復雜的生存資料時尤為顯著,主要由以下幾個內外部因素引起:① 機器學習模型的復雜性增加(例如,深度學習模型具有大量參數和非線性結構),因此為了確保模型能夠有效地泛化和保持穩定性,通常需要更大的樣本量;② 復雜的生存資料涉及更高維度的特征空間,因此需要更多的樣本以充分覆蓋特征空間,以避免過度擬合或欠擬合;③ 機器學習模型通常需要更多的數據進行有效的訓練和調優,這包括捕獲數據中的模式和規律,以及進行參數調整以提高性能;④ 機器學習模型對數據中的噪聲和復雜性更為敏感,更大的樣本量能夠提供更多信息,幫助模型準確區分真實模式和噪聲,從而提高魯棒性和泛化能力。3)過擬合風險高[42]:由于機器學習模型具有足夠的靈活性和參數數量,可以幾乎完美地擬合訓練數據,甚至是其中的噪聲,這種過度擬合會導致模型在訓練數據上表現良好,但在新數據上表現不佳。相比之下,傳統的生存分析模型在一定程度上更加穩定,過擬合的風險較低。關于機器學習的模型更強調采取如交叉驗證、正則化等方式以減少過擬合的風險[43]。除了上述局限性之外,基于機器學習的生存分析模型也存在參數調優困難[44]、計算資源需求高[45]和穩定性差[46]等缺陷。